This article is a step-by-step guide to implement a fairly sophisticated data analysis algorithm, end-to-end in Apache Flink. We will use the PageRank algorithm, an algorithm used for ranking entities in graphs (such as webpages in the web). We will go through Apache Flink's APIs, the Flink iteration feature, optimization, as well as local and distributed execution and monitoring. All code samples are given in both Scala and Java.
The PageRank Algorithm
The original PageRank algorithm became famous as the basis of Google's web search ranking. It determines the importance of a web page compared to other pages in the web graph, making use of the web graph's link structure. Intuitively, it defines that a web page is important if many pages link to it, and these incoming links themselves derive their importance from their originating web page. A common interpretation of PageRank is the "random surfer" analogy: A web surfer that randomly follows links will end up on certain pages with a certain probability. That probability is the PageRank of that web page.
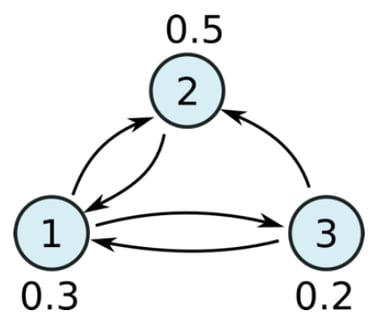
Since its original publication, variations of PageRank has been applied to surprisingly many domains. PageRank has been used to create recommendations (Who to follow on Twitter), for publication disambiguation and word sense disambiguation, and even in biochemistry to find candidate protein interations in the metabolism.
Sample Data
To play around with the PageRank algorithm, virtually any graph data set will do. For validation and debugging purposes, we use a small random data sample, consisting of a handful of nodes and edges. For later evaluations, we use a snapshot of the Twitter follower network. There are various formats in which to represent the graph data. In the course of this article, we assume that the graph is represented through an "adjacency list", where every node is listed together with its outgoing edges.
(page) (link1) (link2)
www.pageUrl.com/site neighbor.org/otherPage www.otherPage.org
www.otherPage.org www.target-page.gov neighbor.org/otherPage
The URLs are used only as identifiers for the pages, and we can use any other type of identifier as well. For the sake of simplicity, we use numbers as identifiers in this article with each number representating a web page:
17 23 42
42 19 23
Enter Apache Flink
Flink is a general-purpose system for parallel data processing, like Hadoop and Spark. Flink has high-level APIs for data analysis programs that can be executed in parallel on a cluster of machines. Flink's APIs offer powerful operations that make it a good match for graph algorithms like PageRank. The core element of Flink's APIs are DataSets, which represent a collection of data elements will be computed and stored in a distributed fashion. Data sets can be loaded for example from (distributed) files or Java/Scala collections, and they are produced by running computations on other data sets.
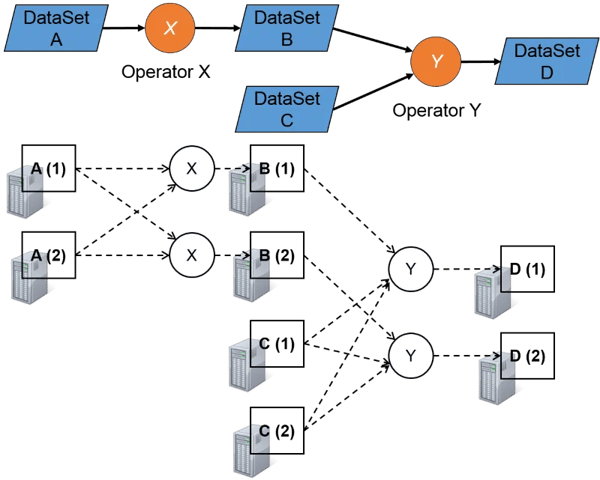
Implementing PageRank
We'll get started by getting some data into Flink. Then, we will create a program that computes one step of the PageRank algorithm. Finally, we will enclose that step in an iteration to complete the algorithm.
One step of PageRank
The following code creates an execution environment (this is the entry hook for Flink programs) and creates our source data set.
def main(args: Array[String]) {
// grab the default execution environment
val env = ExecutionEnvironment.getExecutionEnvironment
// load a data set from a sequence of Java elements
val rawLines : DataSet[String] = env.fromElements(
"1 2 3 4",
"2 1",
"3 5",
"4 2 3",
"5 2 4")
// To run on real data we will use this statement to read the file
// val rawLines = env.readTextFile("hdfs:///demodata/twitter-followers")
}
We can now do a bunch of things with the created data set, like running parallel computations on it, or writing the data somewhere. The following lines tell the system to print the data set to standard output. Note that the env.execute()command triggers the execution - the data sets are not created and no operations are run before that command is called. After those lines are added, we can simply execute this program in our IDE as a Java/Scala application (e.g., by right clicking on the class and choosing "Run").
rawLines.print()
env.execute()Let us now define the parallel computations that together form the PageRank algorithm. We start by defining the data types on which the algorithm works. The Page type refers to a page (identified by its id) with a rank. The Adjacency type defines the neighborhood of a page. It contains the page id and the ids of all neighbors. We add utility constructors and a parse method for convenience.
case class Page(id: Long, rank: Double)
case class Adjacency(id: Long, neighbors: Array[Long])Next, we prepare the data sets on which our algorithm works. So far, our original data set contains a collection of strings that define the adjacent pages for each page. Let us parse these strings and create the proper data types. We also create the initial rank distribution by creating a data set of pages where we assign equal ranks to pages (i.e., each page gets as its rank 1 divided by the number of pages).
val adjacency : DataSet[Adjacency] = rawLines
.map( str => {
val elements = str.split(' ')
val id = elements(0).toLong
val neighbors = elements.slice(1, elements.length).map(_.toLong)
Adjacency(id, neighbors)
} )
val initialRanks : DataSet[Page] = adjacency.map { adj => Page(adj.id, 1.0 / NUM_VERTICES) }With these two data sets, we can now implement the core PageRank step: In the PageRank formula, the new rank of a page is the sum of the ranks of the neighboring pages that point to it (weighted by how many outgoing links the source pages have, and the dampening factor). We implement this in two operations:
-
Each page distributes its rank to all the neighbors. The page takes its total rank, divides it by the number of neighbors and "contributes" that partial rank to all its neighbors.
-
For each page, we sum up those partial ranks, to get the new rank.
To reproduce the PageRank formula correctly, we need to account for the dampening factor and the random jump. We apply the dampening factor when the ranks are distributed to the neighbors. Every page contributes the random jump to itself - that way this term is created exactly once for each page, including those that have no pages that point to them.
// define some constants for the page rank algorithm
private final val DAMPENING_FACTOR: Double = 0.85
private final val NUM_VERTICES = 82140L;
private final val RANDOM_JUMP = (1-DAMPENING_FACTOR) / NUM_VERTICES;
val rankContributions = initialPages.join(adjacency).where("id").equalTo("id") {
// we run a "flat join" that takes the left and right types (here page and adj)
// and produces multiple result elements
(page, adj, out : Collector[Page]) => {
val rankPerTarget = DAMPENING_FACTOR * page.rank / adj.neighbors.length;
// send random jump to self
out.collect(Page(page.id, RANDOM_JUMP))
// partial rank to each neighbor
for (neighbor <- adj.neighbors) {
out.collect(Page(neighbor, rankPerTarget));
}
}
}
val newRanks = rankContributions .groupBy("id").reduce( (a,b) => Page(a.id, a.rank + b.rank) )With those steps, we have the core step of the PageRank Algorithm in place. If we print the results and execute program, we see the approximation of the ranks after one step:
1: 0.2
2: 0.2566666666666667
3: 0.17166666666666666
4: 0.1716666666666667
5: 0.2
Making the Algorithm iterative
To create the iterative variant of the algorithm, we use Flink's iteration construct to define the loop. We create an IterativeDataSet and use it as the basis of the page rank step. After the PageRank step, we "close the loop" with the data set containing the new ranks. Closing the loop tells the system to use the new ranks the next time it executes the PageRank step. Note how the code below uses the iterative set pages in the computation of the rankContributions and later closes the iteration with the newRanks data set. Note that in Scala, we make use of Scala's concise functional syntax and embed the iteration step in a nested function of type DataSet[Page] => DataSet[Page]. The function takes the iterative data set and returns the one that is used to close the loop.
val iteration = initialRanks.iterate(numIterations) {
pages => {
val rankContributions = pages.join(adjacency).where("id").equalTo("id") {
(page, adj, out : Collector[Page]) => {
val rankPerTarget = DAMPENING_FACTOR*page.rank/adj.neighbors.length;
// send random jump to self
out.collect(Page(page.id, RANDOM_JUMP))
// partial rank to each neighbor
for (neighbor <- adj.neighbors) {
out.collect(Page(neighbor, rankPerTarget));
}
}
}
rankContributions.groupBy("id").reduce( (a,b) => Page(a.id, a.rank + b.rank)) } }If we run this program in our IDE and look at the log in the console, we see some messages that the operations start and finish their iterations (sample), and we see a final result:
INFO task.IterationIntermediatePactTask: starting iteration [22]: Join (flink.tutorial.pagerank.PageRank$3) (1/4)
INFO task.IterationIntermediatePactTask: finishing iteration [22]: Join (flink.tutorial.pagerank.PageRank$3) (1/4)
INFO task.IterationIntermediatePactTask: starting iteration [22]: Join (flink.tutorial.pagerank.PageRank$3) (4/4)
INFO task.IterationIntermediatePactTask: finishing iteration [22]: Join (flink.tutorial.pagerank.PageRank$3) (4/4)
INFO task.IterationTailPactTask: finishing iteration [22]: Reduce(flink.tutorial.pagerank.PageRank$4) (1/4)
INFO task.IterationTailPactTask: finishing iteration [22]: Reduce(flink.tutorial.pagerank.PageRank$4) (2/4)
1: 0.2380722058798589
2: 0.24479082825856807
3: 0.17046158206611492
4: 0.17178303768658085
5: 0.17489234610887724
Note that we used a fixed number of iterations. There are various ways to extend the algorithm to check for convergence and terminate accordingly.
On large data
To try the algorithm on a real data set, we run it over the Twitter follower graph described in the introduction. We read the adjacency lists as a text file and keep the remainder of the algorithm unchanged.
DataSet rawLines = env.readTextFile("hdfs:///demodata/twitter-followers");
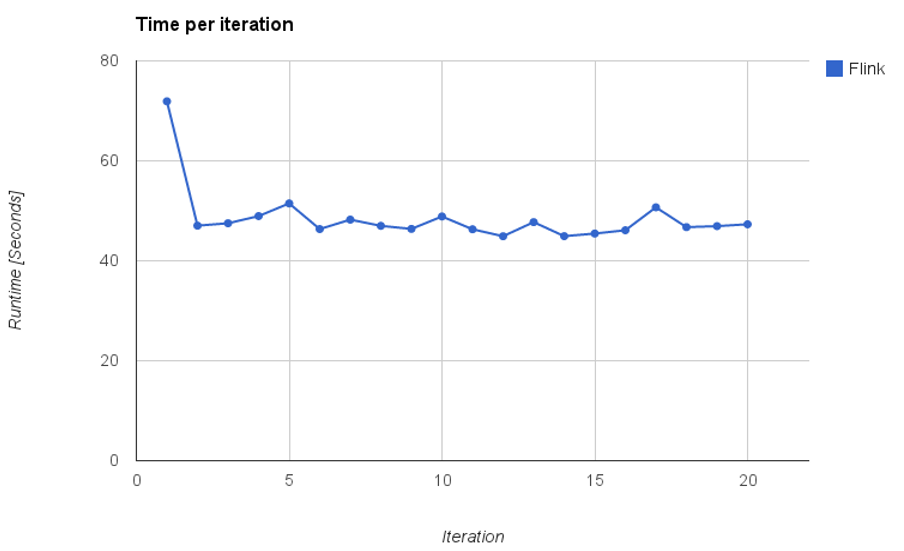
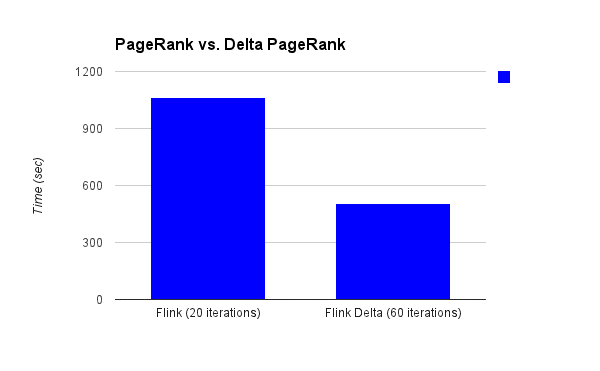
The graph has 41,652,230 nodes (users) and 1,468,365,182 edges (followings). The chart below shows the runtimes on a small cluster setup of 24 machines with 8 cores with 20 GiBytes of main memory for each machine. The execution time of the first iteration is larger, because it includes the initial preparatory operations.
Looking at our Program
To get a better understanding of our program, we examine it in Flink's plan visualization tool. Flink can dump a JSON representation of the program's data flow and render it in a web browser. We simply replace the statement env.execute() withSystem.out.println(env.getExecutionPlan()) and run the program to get a printout of the JSON dump. We paste the JSON on the pagetools/planVisualizer.html in the Flink home folder.
In the program plan, each small box represents an operation and between the operations, we see at which points the system shuffles and sorts data. The large box represents the iteration. We can see that the join uses a hash join strategy and the hash table is cached across iterations.
Going further - Delta Page Rank
While the above presented variant of PageRank performs already well, there is a way to further improve it significantly by using one of Apache Flink's unique features: stateful iterations. The PageRank algorithm exhibits two characteristics that most graphs (and machine learning) algorithms exhibit in practice: sparse computational dependencies and asymmetric convergence. To illustrate that, let us look at the actual changes that PageRank computes in each iteration. The graph below shows how many nodes in the graph actually change their rank by more than a certain minimal threshold (on a sample graph of 80,000 nodes). One can see that most nodes change their rank only in the first few iterations and remain stable afterwards.
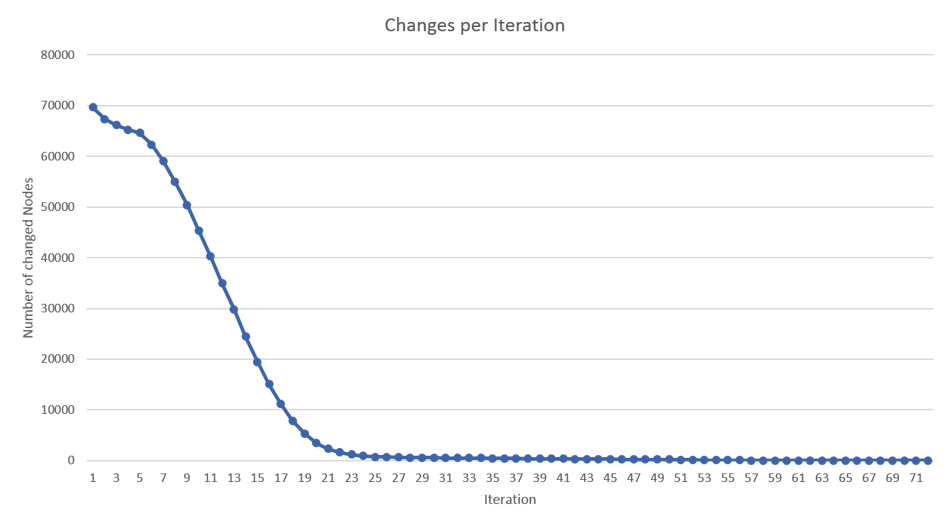
If we can change the algorithm such that it works only with the changed vertices, in each step, we can significantly improve the algorithm runtime. In fact, much of the design of graph processing systems like Apache Giraph and GraphLab was made exactly to exploit those characteristics.
Delta PageRank Algorithm
The first step to exploit that characteristic is to rewrite the algorithm to work with rank deltas, rather than with the absolute rank values. In each iteration, nodes send delta changes to other nodes (depending on their own change) and sum up the deltas to the final delta, which is added to the current value. The code below shows the core of the delta PageRank algorithm, which is only slightly different from the original version above. The second operation adds up all partial deltas and filters the final delta by a threshold. Note that we are not using the Page and Adjacency classes here, because Flink's delta iterations support only tuples in the current release. We use 2-tuples (page-id, rank) instead of Page and (page-id, neighbors[]) instead of Adjacency.
val deltas = workset.join(adjacency).where(0).equalTo(0) {
(lastDeltas, adj, out : Collector[Page]) => {
val targets = adj._2;
val deltaPerTarget = DAMPENING_FACTOR * lastDeltas._2 / targets.length;
for (target <- targets) {
out.collect((target, deltaPerTarget));
}
}}
.groupBy(0).sum(1)
.filter( x => Math.abs(x._2) > THRESHOLD );
val rankUpdates = solutionSet.join(deltas).where(0).equalTo(0) { (current, delta) => (current._1, current._2 + delta._2) }These functions compute the deltas in each iteration based on the deltas in the previous iteration. To find our initial deltas, we run one step of the regular PageRank algorithm over the uniformly initialized ranks. Our first deltas are the differences between the result of that step and the uniform ranks. The last piece that we need, is a way to keep unmodified nodes (pages) around as “state” across the iterations - Flink’s Delta Iterations can do that for us.
Delta Iterations in Apache Flink
Delta iterations in Flink privide functionality to split the iteration between state and workset. The state (otherwise called solution set) is where we keep the result that we actually want to compute, while the workset carries the data that drives the next iteration. In our case, the state is the data set of pages with their ranks, while the workset is the computed and filtered deltas.
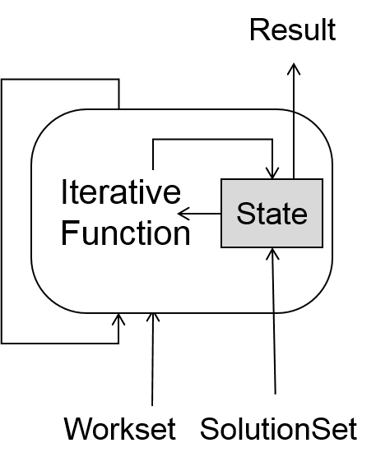
The solution set is a distributed key/value data set that is partitioned over many machines. We can access it by joining (or co-grouping) with the data set on its key. To change or add elements to the solution set, we simply create a new data set (the solution set updates) that contains the new or updated elements. At the end of each iteration these updates are merged into the solution set, where elements replace previous entries with the same key (or are added, if no prior entry with the key existed). For our PageRank algorithm, we use the page id as the key. At the end of each iteration, we create a data set that contains the pages whose rank changed (the updates) and deltas to be used in the next iteration (the next workset). At runtime, Flink automatically keeps the solution set partitioned in an index. That way, joins with the solution set become index lookups, and updates to the solution set become index insertions/updates. For us that means that if a node is not used inside one iteration (because it is converged and did not change), its data is not accessed at all - it simply remains untouched in the index. Here is the final code for PageRank as a delta iteration:
object DeltaPageRank {
private final val DAMPENING_FACTOR: Double = 0.85
private final val NUM_VERTICES = 82140L
private final val INITIAL_RANK = 1.0 / NUM_VERTICES
private final val RANDOM_JUMP = (1-DAMPENING_FACTOR) / NUM_VERTICES
private final val THRESHOLD = 0.0001 / NUM_VERTICES
type Page = (Long, Double)
type Adjacency = (Long, Array[Long])
def main(args: Array[String]) {
val numIterations = 30;
val adjacencyPath = "/path/to/adjacency.csv";
val outpath = "/path/to/out.txt";
val env = ExecutionEnvironment.getExecutionEnvironment
val adjacency : DataSet[Adjacency] = env.readTextFile(adjacencyPath)
.map( str => {
val elements = str.split(' ')
val id = elements(0).toLong
val neighbors = elements.slice(1, elements.length).map(_.toLong)
(id, neighbors)
} )
val initialRanks : DataSet[Page] = adjacency.flatMap {
(adj, out : Collector[Page]) => {
val targets = adj._2
val rankPerTarget = INITIAL_RANK * DAMPENING_FACTOR / targets.length
// dampend fraction to targets
for (target <- targets) {
out.collect((target, rankPerTarget))
}
// random jump to self
out.collect((adj._1, RANDOM_JUMP));
}
}
.groupBy(0).sum(1);
val initialDeltas = initialRanks.map
{ (page) => (page._1, page._2 - INITIAL_RANK) }
val iteration = initialRanks.iterateDelta(initialDeltas, 100, Array(0) ) {
(solutionSet, workset) => {
val deltas = workset.join(adjacency).where(0).equalTo(0) {
(lastDeltas, adj, out : Collector[Page]) => {
val targets = adj._2;
val deltaPerTarget =
DAMPENING_FACTOR * lastDeltas._2 / targets.length;
for (target <- targets) {
out.collect((target, deltaPerTarget));
}
}
}
.groupBy(0).sum(1)
.filter( x => Math.abs(x._2) > THRESHOLD );
val rankUpdates = solutionSet.join(deltas).where(0).equalTo(0) {
(current, delta) => (current._1, current._2 + delta._2)
}
(rankUpdates, deltas)
}
}
iteration.writeAsCsv(outpath, writeMode = WriteMode.OVERWRITE)
env.execute("Page Rank"); } }Performance
We run the delta-PageRank on the Twitter follower data set with the same setup. The graph below shows that the revised algorithm is out of the box twice as fast as the original algorithm. Looking closer, we see that it actually ran 60 iterations until it found that all deltas are small enough to consider the state converged, which makes the speedup compared to the 20 plain iterations (without convergence check) more significant.
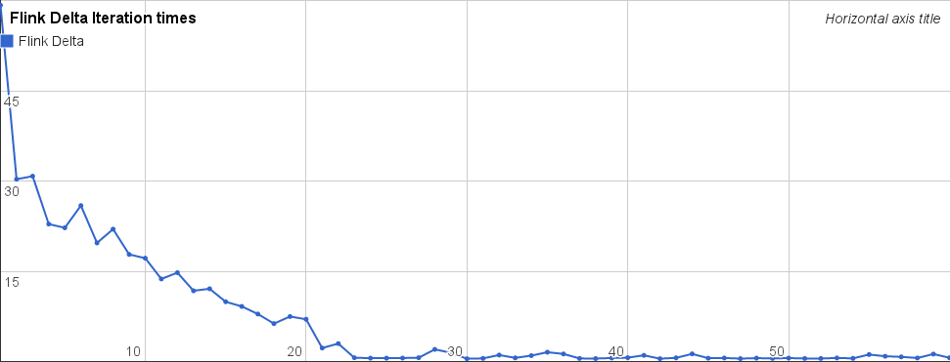
Digging into the times spent in each iteration (chart below), we can see that the algorithm shows the expected behavior: The time spent in each iteration decreases quickly, and the long tail of the iterations take very little time each.
Formal Definition and Algorithm
Formally, the PageRank PR(pi) of a webpage pi is defined through the following formula:
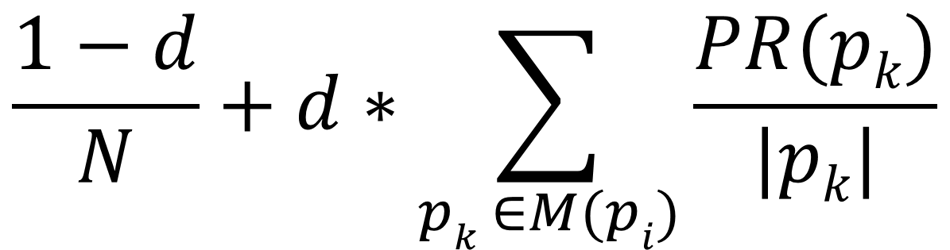
where |pi| denotes the number of outgoing links of node pi, and M(pi) denotes all nodes that have links to node pi. Note that this formula introduces a so called "dampening factor" (d) and "random jump" term (the first term). This describes the probability that a random surfer leaves his current sequence of randomly following links and starts a new run somewhere else. The solution for this recursive definition (the PageRank of a node depends on the PageRank of neighbor nodes) for the graph as a whole is equilibrium probability distribution of the Markov chain described by the nodes (states) and links (transitions). As such, it can be numerically computed using a so-called "power method": We start with a random distribution and repeatedly compute the ranks of all nodes, referring to the previous solution, until the probabilities do not change any more. For an analogy, picture throwing a huge amount of random surfers onto the graph and let then surf in parallel. After a while, the number of surfers on each page at any point in time will be stable and define the rank of that page.
From Kappa Architecture to Streamhouse: Making the Lakehouse Real-Time
Fluss Is Now Open Source
Announcing Ververica Platform: Self-Managed 2.14
